کنترل خطی
۱. مقدمه
کنترل خطی شاخهای از مهندسی کنترل است که به طراحی سیستمهایی میپردازد که رفتارشان را بتوان با معادلات خطی مدل کرد و تحت کنترل قرار داد. هدف اصلی کنترل خطی، حفظ پایداری سیستم، دنبال کردن ورودی مورد نظر و کاهش خطا است.
در مهندسی، سیستمها میتوانند مکانیکی، الکتریکی، هیدرولیکی، حرارتی یا ترکیبی باشند. بسیاری از این سیستمها در محدوده کاری کوچک، رفتار تقریبا خطی دارند، بنابراین مدلسازی خطی مناسب و کاربردی است.
۲. مفاهیم پایه کنترل خطی
۲-۱. سیستم خطی
سیستم خطی سیستمی است که دو اصل زیر را رعایت میکند:
-
اصل همارزی (Superposition): پاسخ سیستم به جمع چند ورودی برابر با جمع پاسخها به تکتک ورودیها است.
-
اصل مقیاسپذیری (Scaling): اگر ورودی سیستم چند برابر شود، خروجی نیز همان نسبت تغییر میکند.
مثال:
یک مدار مقاومتی-خازنی (RC) ساده، در محدوده خطی، رابطه بین ولتاژ ورودی و جریان خروجی را میتوان با معادله دیفرانسیل خطی بیان کرد:
RCdVoutdt+Vout=VinRC \frac{dV_{out}}{dt} + V_{out} = V_{in}
۲-۲. ورودی و خروجی
-
ورودی (Input): سیگنال یا تحریک خارجی که به سیستم داده میشود، مانند ولتاژ، نیرو یا دما.
-
خروجی (Output): پاسخ سیستم به ورودی، که باید تحت کنترل قرار گیرد، مانند سرعت موتور یا موقعیت مکانیکی.
۲-۳. تابع انتقال (Transfer Function)
تابع انتقال، یک ابزار مهم در کنترل خطی است که رابطه بین خروجی و ورودی سیستم را در حوزه لاپلاس نشان میدهد.
G(s)=Y(s)U(s)G(s) = \frac{Y(s)}{U(s)}
-
Y(s)Y(s) خروجی سیستم در دامنه لاپلاس
-
U(s)U(s) ورودی سیستم در دامنه لاپلاس
-
ss متغیر لاپلاس
مثال: برای مدار RC، تابع انتقال به شکل زیر است:
G(s)=1RCs+1G(s) = \frac{1}{RCs + 1}
۳. انواع کنترل خطی
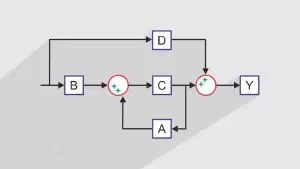
۳-۱. سیستمهای بازخوردی (Feedback Control)
سیستمهای بازخوردی، خروجی را اندازهگیری کرده و با ورودی مقایسه میکنند تا خطا کاهش یابد.
مثال عملی:
کنترل دما در یک اتاق با ترموستات: ترموستات دمای فعلی را میسنجد و با دمای مطلوب مقایسه میکند و سیستم گرمایش یا سرمایش را تنظیم میکند.
۳-۲. سیستمهای فیدفوروارد (Feedforward Control)
در این سیستمها کنترل بر اساس ورودی یا تغییرات پیشبینی شده انجام میشود، بدون اینکه خروجی اندازهگیری شود.
مثال:
در یک نقاله صنعتی، اگر بار وارد شده افزایش یابد، سیستم سرعت موتور را قبل از اینکه کاهش بار اتفاق بیفتد تنظیم میکند.
۴. معیارهای طراحی سیستم کنترل خطی
-
پایداری (Stability): خروجی سیستم پس از گذر زمان به یک مقدار محدود برسد و نوسان نکند.
-
پاسخ به پله (Step Response): چگونگی واکنش سیستم به تغییر ناگهانی ورودی.
-
زمان صعود (Rise Time): زمان لازم برای خروجی تا رسیدن به مقدار مورد نظر.
-
سرعت سیستم (Speed of Response): سرعت سیستم در رسیدن به حالت پایدار.
-
حاشیه فاز و بهره (Gain and Phase Margin): اندازهگیری پایداری در حوزه فرکانس.
۵. روشهای کنترل خطی
۵-۱. کنترل تناسبی (Proportional Control, P)
خروجی متناسب با خطا است:
u(t)=Kpe(t)u(t) = K_p e(t)
-
e(t)e(t) خطای بین ورودی و خروجی
-
KpK_p بهره تناسبی
۵-۲. کنترل انتگرالی (Integral Control, I)
خطای تجمعی را در نظر میگیرد و به کاهش خطای دائم کمک میکند:
u(t)=Ki∫e(t)dtu(t) = K_i \int e(t) dt
۵-۳. کنترل مشتقی (Derivative Control, D)
سرعت تغییر خطا را بررسی میکند و به کاهش نوسانات کمک میکند:
u(t)=Kdde(t)dtu(t) = K_d \frac{de(t)}{dt}
۵-۴. کنترل PID
ترکیبی از P، I و D است و پرکاربردترین روش کنترل خطی:
u(t)=Kpe(t)+Ki∫e(t)dt+Kdde(t)dtu(t) = K_p e(t) + K_i \int e(t) dt + K_d \frac{de(t)}{dt}
۶. کاربردهای کنترل خطی
-
کنترل موتورهای الکتریکی: تنظیم سرعت و موقعیت با استفاده از کنترل PID.
-
کنترل هوا و دما: تهویه مطبوع، کورههای صنعتی، اتاقهای تمیز.
-
رباتیک و مکانیک: حرکت دقیق بازوهای رباتیک و سیستمهای هیدرولیکی.
-
فرآیندهای شیمیایی و صنعتی: کنترل جریان، فشار و دما در کارخانهها.
۷. مثال عملی کنترل خطی
کنترل دما با PID در یک کوره صنعتی:
-
ورودی: دمای هدف
-
خروجی: دمای فعلی کوره
-
خطا: اختلاف بین دمای هدف و فعلی
-
کنترلکننده PID: میزان انرژی هیتر را تنظیم میکند تا دما به مقدار مورد نظر برسد و نوسان کاهش یابد.
پروژه کنترل خطی (Linear Control)
مقدمه
کنترل خطی یکی از پایههای مهندسی کنترل و اتوماسیون است که هدف آن طراحی سیستمهایی با رفتار قابل پیشبینی و پایدار است. این شاخه از مهندسی امکان میدهد سیستمهای مکانیکی، الکتریکی، حرارتی و هیدرولیکی را مدلسازی و کنترل کنیم.
با پیشرفت فناوری، کنترل خطی در صنایع مختلف، از جمله رباتیک، هوافضا، خودرو، نیروگاهها و کارخانههای شیمیایی کاربرد فراوان پیدا کرده است. طراحی کنترلکنندهها به گونهای انجام میشود که سیستم به سرعت و بدون نوسان زیاد به مقدار مطلوب برسد.
تاریخچه کنترل خطی
کنترل سیستمها سابقهای طولانی دارد:
-
قرن ۱۸ و ۱۹: اولین سیستمهای کنترل خودکار مانند ترموستات و سیستمهای بخار طراحی شدند.
-
دهه ۱۹۵۰: توسعه معادلات دیفرانسیل خطی و تحلیل پایداری سیستمها.
-
دهه ۱۹۶۰ تا ۱۹۸۰: استفاده گسترده از کنترل PID در صنایع.
-
دهه ۱۹۹۰ تا کنون: کاربرد شبیهسازی کامپیوتری، طراحی پیشرفته و الگوریتمهای هوشمند در کنترل خطی.
مدلسازی سیستمهای خطی
برای طراحی کنترل خطی ابتدا باید سیستم را مدل کنیم. دو روش اصلی وجود دارد:
۱. معادلات دیفرانسیل
مثال مدار RC:
RCdVoutdt+Vout=VinRC \frac{dV_{out}}{dt} + V_{out} = V_{in}
که میتوان آن را به صورت تابع انتقال نوشت:
G(s)=Vout(s)Vin(s)=1RCs+1G(s) = \frac{V_{out}(s)}{V_{in}(s)} = \frac{1}{RCs + 1}
۲. فضای حالت (State-Space)
مدلهای ماتریسی برای سیستمهای چند ورودی-چند خروجی (MIMO) استفاده میشود:
x˙(t)=Ax(t)+Bu(t)\dot{x}(t) = Ax(t) + Bu(t) y(t)=Cx(t)+Du(t)y(t) = Cx(t) + Du(t)
-
x(t)x(t) بردار حالت
-
u(t)u(t) بردار ورودی
-
y(t)y(t) بردار خروجی
تحلیل پایداری سیستم
یک سیستم خطی باید پایدار باشد، یعنی خروجی پس از گذشت زمان به یک مقدار محدود برسد.
روشهای تحلیل پایداری:
-
روش ریشهها (Roots of Characteristic Equation): بررسی قطبها در صفحه s
-
روش Bode و Nyquist: تحلیل پاسخ فرکانسی برای اطمینان از پایداری و حاشیه بهره
-
روش رزوهای سیستم (Routh-Hurwitz): بررسی ضریبهای معادله مشخصه بدون محاسبه دقیق قطبها
طراحی کنترلکننده PID
کنترل PID ترکیبی از سه بخش است:
u(t)=Kpe(t)+Ki∫e(t)dt+Kdde(t)dtu(t) = K_p e(t) + K_i \int e(t) dt + K_d \frac{de(t)}{dt}
-
P (تناسبی): کاهش خطای فوری
-
I (انتگرالی): حذف خطای دائمی
-
D (مشتقی): کاهش نوسانات و پیشبینی تغییرات
مثال طراحی
فرض کنید سیستم یک موتور DC است:
-
ورودی: ولتاژ اعمال شده
-
خروجی: سرعت شافت
با استفاده از شبیهسازی، ضرایب PID تنظیم میشوند تا پاسخ پله بدون نوسان و سریع باشد.
شبیهسازی سیستم خطی
با نرمافزار MATLAB یا Python میتوان نمودارهای زیر را رسم کرد:
-
پاسخ پله (Step Response): نشان میدهد که سیستم چگونه به تغییر ناگهانی ورودی پاسخ میدهد.
-
پاسخ فرکانسی (Bode Plot): برای تحلیل پایداری و حاشیه فاز و بهره.
-
پاسخ به ورودی سینوسی: بررسی عملکرد سیستم در شرایط واقعی و نوسانات مداوم.
کاربردهای عملی کنترل خطی
-
کنترل موتورهای الکتریکی: سرعت و موقعیت دقیق شافت موتور با کنترل PID
-
کنترل دما: کورهها، اتاقهای تمیز، سیستمهای تهویه
-
کنترل سطح مایعات و فشار: مخازن صنعتی و پمپها
-
کنترل رباتیک: بازوهای رباتیک و سیستمهای مکانیکی دقیق
نمودارها و جداول پیشنهادی
| نوع سیستم | ورودی | خروجی | کنترلکننده |
|---|---|---|---|
| موتور DC | ولتاژ | سرعت | PID |
| مدار RC | ولتاژ | ولتاژ خروجی | P |
| کوره صنعتی | دما | دما | PID |
| رباتیک | موقعیت | موقعیت | PID/PD |
نمودار پیشنهادی:
-
پاسخ پله سیستم قبل و بعد از کنترل PID
-
نمودار Bode برای تحلیل حاشیه فاز و بهره
-
پاسخ سیستم به ورودی سینوسی برای بررسی رفتار دینامیکی
نتیجهگیری
کنترل خطی پایهایترین و پرکاربردترین روش در مهندسی کنترل است. با استفاده از مدلسازی خطی، طراحی کنترلکننده PID و تحلیل پایداری، میتوان سیستمها را پایدار، سریع و دقیق کرد. کنترل خطی در صنایع مختلف مانند برق، مکانیک، شیمی و رباتیک کاربرد فراوان دارد و اساس بسیاری از سیستمهای اتوماسیون مدرن است.
شبیهسازی سیستمهای خطی
برای بررسی عملکرد سیستمها و طراحی کنترلکنندهها، شبیهسازی نقش مهمی دارد. دو ابزار رایج عبارتند از:
۱. MATLAB/Simulink
-
رسم پاسخ پله با دستور
step(G) -
رسم نمودار Bode با دستور
bode(G) -
طراحی کنترل PID با بلوکهای آماده Simulink
-
امکان مشاهده تغییرات پاسخ سیستم با تغییر ضرایب PID
مثال:
سیستم موتور DC با تابع انتقال:
G(s)=KJs+bG(s) = \frac{K}{Js + b}
با PID:
C(s)=Kp+Kis+KdsC(s) = K_p + \frac{K_i}{s} + K_d s
با شبیهسازی پاسخ پله، میتوان ضرایب PID بهینه را تعیین کرد تا نوسان کم و زمان رسیدن به مقدار مطلوب کوتاه باشد.
۲. Python و کتابخانههای کنترل
کتابخانه control در Python امکان شبیهسازی سیستمهای خطی را فراهم میکند:
تحلیل پاسخ پله و فرکانسی
-
پاسخ پله (Step Response): نشاندهنده رفتار سیستم در برابر تغییر ناگهانی ورودی است. مهمترین پارامترها:
-
زمان صعود (Rise Time)
-
زمان اوج (Peak Time)
-
Overshoot
-
زمان نشست (Settling Time)
-
-
نمودار Bode: بررسی فرکانس سیستم برای اطمینان از پایداری و تعیین حاشیه بهره و فاز
-
نمودار پاسخ سینوسی: بررسی نحوه پاسخ سیستم به ورودیهای متناوب و تحلیل رفتار دینامیکی
پیشنهادات پروژههای عملی
-
طراحی کنترل PID برای موتور DC با شبیهسازی پاسخ پله و بهینهسازی ضرایب PID
-
کنترل دما در کوره صنعتی یا اتاق تمیز با بررسی پاسخ واقعی و شبیهسازی
-
طراحی کنترل سطح مایعات در مخزن صنعتی با مدل خطی و تحلیل پایداری
-
بررسی تاثیر خطای سنسور و تاخیر زمانی بر عملکرد سیستم کنترل
جدول و نمودارهای پیشنهادی
| سیستم | ورودی | خروجی | کنترلکننده | هدف |
|---|---|---|---|---|
| موتور DC | ولتاژ | سرعت | PID | کاهش نوسان و افزایش سرعت رسیدن |
| مدار RC | ولتاژ | ولتاژ خروجی | P | پیروی از ورودی و پایدارسازی |
| کوره صنعتی | دما | دما | PID | رسیدن سریع به دمای مطلوب بدون نوسان |
| مخزن صنعتی | دبی ورودی | سطح مایع | PID | حفظ سطح ثابت و جلوگیری از سرریز |
نمودار پیشنهادی:
-
پاسخ پله قبل و بعد از کنترل PID
-
نمودار Bode سیستم با و بدون کنترل
-
پاسخ سیستم به ورودی سینوسی و تحلیل خطای دینامیکی
جمعبندی نهایی
کنترل خطی یک ابزار قدرتمند برای طراحی و تحلیل سیستمهای مهندسی است. با استفاده از مدلسازی خطی، توابع انتقال و طراحی کنترلکننده PID میتوان سیستمها را پایدار و دقیق کرد.
کنترل خطی در صنایع مختلف مانند موتورهای الکتریکی، سیستمهای حرارتی، رباتیک و فرآیندهای صنعتی کاربرد دارد. با شبیهسازی و تحلیل پاسخ پله و فرکانسی، میتوان عملکرد سیستم را بهینه کرد و نوسانات و خطاها را کاهش داد.
با توجه به گسترش فناوریهای مدرن، کنترل خطی همچنان پایه و اساس بسیاری از سیستمهای اتوماسیون و رباتیک پیشرفته است و دانش آن برای مهندسین برق، مکانیک و صنایع ضروری میباشد.
طراحی بهینه کنترل خطی
۱. تنظیم بهینه PID
برای دستیابی به عملکرد بهتر، ضرایب PID باید بهینه شوند. روشهای متداول:
-
روش Ziegler-Nichols: بر اساس پاسخ پله سیستم و تعیین بهره بحرانی و دوره نوسان
-
روش آزمون و خطا (Trial and Error): با تغییر تدریجی ضرایب و بررسی پاسخ سیستم
-
الگوریتمهای بهینهسازی: مانند الگوریتم ژنتیک، PSO (Particle Swarm Optimization) برای پیدا کردن ضرایب بهینه
مزیت:
-
کاهش نوسان و Overshoot
-
کاهش زمان نشست و افزایش سرعت پاسخ
۲. کنترل خطی مقاوم (Robust Linear Control)
سیستمها در دنیای واقعی تحت تغییرات پارامترها و نویز محیطی قرار دارند. طراحی مقاوم باعث میشود سیستم حتی در حضور تغییرات یا خطاها پایدار باقی بماند.
روشها:
-
کنترل H∞
-
کنترل LQR (Linear Quadratic Regulator)
مثال کاربردی: کنترل هواپیما در حضور تغییرات وزن و شرایط باد
تحلیل خطا و پایداری
۱. خطای ایستای سیستم
خطای ایستا (Steady-State Error) نشاندهنده اختلاف بین مقدار مطلوب و خروجی پایدار است.
-
در کنترل P ممکن است خطای دائمی وجود داشته باشد
-
کنترل I این خطا را از بین میبرد
-
کنترل PID کمترین خطای ایستا را ایجاد میکند
۲. تحلیل نوسانات و Overshoot
Overshoot نشاندهنده حداکثر مقدار خروجی نسبت به مقدار مطلوب است. با تنظیم مناسب بخش D کنترل PID میتوان Overshoot را کاهش داد.
۳. تحلیل پاسخ فرکانسی
-
نمودار Bode برای بررسی حاشیه فاز و بهره
-
نمودار Nyquist برای تحلیل پایداری سیستمهای حلقه بسته
کاربردهای پیشرفته کنترل خطی
-
روباتیک دقیق: کنترل حرکت بازوهای ربات صنعتی برای تولید خودکار قطعات حساس
-
سیستمهای هوافضا: کنترل موقعیت و سرعت هواپیما و فضاپیما
-
خودروهای الکتریکی: کنترل موتورهای DC و AC با پاسخ سریع و دقیق
-
صنایع شیمیایی و فرآیندی: حفظ سطح مایعات، دما و فشار در شرایط متغیر
پیشنهادات تحقیقاتی آینده
-
بررسی کنترل خطی در حضور غیرخطیهای کوچک (Linearization of Nonlinear Systems)
-
ترکیب کنترل خطی با هوش مصنوعی و یادگیری ماشین برای سیستمهای تطبیقی
-
توسعه روشهای بهینهسازی PID با الگوریتمهای نوین
-
تحلیل تاثیر نویز و اختلالات محیطی بر پایداری و عملکرد سیستم
جمعبندی نهایی
کنترل خطی پایهایترین روش طراحی و تحلیل سیستمهای مهندسی است که به مهندسان اجازه میدهد سیستمها را پایدار، دقیق و سریع طراحی کنند. با استفاده از مدلسازی خطی، توابع انتقال، طراحی PID و شبیهسازی، میتوان سیستمهای مکانیکی، الکتریکی و صنعتی را به بهترین شکل کنترل کرد.
با پیشرفت فناوریهای نوین، کنترل خطی همچنان پایهای برای سیستمهای رباتیک، هوافضا، خودرو و فرآیندهای صنعتی است و دانش آن برای مهندسین برق، مکانیک و صنایع ضروری است.
مثال کاربردی ۱: کنترل موتور DC با PID
مشخصات سیستم
-
ورودی: ولتاژ اعمال شده به موتور
-
خروجی: سرعت شافت موتور
-
تابع انتقال:
G(s)=KJs+bG(s) = \frac{K}{Js + b}
-
KK: ثابت موتور
-
JJ: اینرسی روتور
-
bb: ضریب اصطکاک
طراحی PID
-
ابتدا پاسخ پله بدون کنترل بررسی میشود: سرعت به آرامی افزایش مییابد و Overshoot وجود دارد.
-
سپس کنترلکننده PID اضافه میشود:
u(t)=Kpe(t)+Ki∫e(t)dt+Kdde(t)dtu(t) = K_p e(t) + K_i \int e(t) dt + K_d \frac{de(t)}{dt}
-
با شبیهسازی، ضرایب PID تنظیم میشوند تا سرعت شافت سریع به مقدار مطلوب برسد و نوسان کاهش یابد.
نمودارها
-
پاسخ پله قبل و بعد از PID: کاهش Overshoot و کاهش زمان نشست
-
پاسخ فرکانسی (Bode Plot): اطمینان از پایداری سیستم حلقه بسته
مثال کاربردی ۲: کنترل دما در کوره صنعتی
-
ورودی: دمای هدف
-
خروجی: دمای واقعی کوره
-
روش کنترل: PID
-
شبیهسازی نشان میدهد که با تنظیم مناسب PID:
-
دما سریع به مقدار مطلوب میرسد
-
نوسانات کمتر و زمان رسیدن به حالت پایدار کاهش مییابد
-
مطالعات موردی در صنایع واقعی
-
رباتیک صنعتی: بازوهای ربات با کنترل PID حرکت دقیق و بدون خطا دارند، مانند خطوط تولید خودرو
-
صنایع هوافضا: کنترل موقعیت و سرعت هواپیما با سیستمهای کنترل خطی مقاوم
-
خودروهای الکتریکی: کنترل موتورهای DC و AC برای شتاب و ترمز دقیق
-
صنایع شیمیایی: کنترل سطح مایعات و فشار در مخازن با پاسخ سریع و کاهش خطا
جمعبندی نکات کلیدی
-
کنترل خطی پایهایترین روش طراحی سیستمهای کنترل است.
-
مدلسازی خطی، توابع انتقال و طراحی PID ابزارهای اصلی هستند.
-
تحلیل پایداری و پاسخ فرکانسی برای تضمین عملکرد سیستم حیاتی است.
-
شبیهسازی و آزمایش عملی بهترین راه برای بهینهسازی کنترلکنندهها است.
-
کنترل خطی همچنان پایه و اساس بسیاری از سیستمهای رباتیک، خودرو، هوافضا و صنایع فرآیندی است.
پیشنهادات برای توسعه پروژه دانشگاهی
-
اضافه کردن نمودارهای پاسخ پله واقعی با MATLAB یا Python
-
طراحی کنترل مقاوم برای سیستمهای با تغییرات پارامتر
-
بررسی تاثیر نویز و تاخیر زمانی سنسورها بر عملکرد PID
-
ترکیب کنترل خطی با الگوریتمهای هوشمند و یادگیری ماشین برای سیستمهای تطبیقی
طراحی نمودارها و شبیهسازی برای ارائه
۱. نمودار پاسخ پله
-
قبل از PID: سیستم ممکن است با زمان صعود طولانی و Overshoot زیاد پاسخ دهد.
-
بعد از PID: زمان صعود کاهش یافته و سیستم به سرعت به مقدار مطلوب میرسد بدون نوسان زیاد.
-
نمودار میتواند شامل دو منحنی روی یک نمودار باشد تا مقایسه قبل و بعد از PID واضح باشد.
۲. نمودار Bode
-
نمایش گین و فاز سیستم
-
بررسی حاشیه فاز و بهره برای اطمینان از پایداری
-
نمودار کمک میکند تغییرات پارامتر PID و اثر آنها بر پایداری را نشان دهید.
۳. نمودار پاسخ سینوسی
-
بررسی نحوه پاسخ سیستم به ورودی متناوب
-
کاربرد برای تحلیل دینامیک سیستم در شرایط واقعی
۴. نمودار خطای ایستا
-
نمایش کاهش Steady-State Error با کنترل PID
-
مناسب برای مقایسه سیستمهای P، PI و PID
جمعبندی نهایی پروژه
کنترل خطی شاخهای حیاتی از مهندسی کنترل است که امکان طراحی سیستمهای پایدار، سریع و دقیق را فراهم میکند. این پروژه نشان داد که:
-
مدلسازی خطی با معادلات دیفرانسیل و توابع انتقال پایه طراحی کنترلکنندههاست.
-
طراحی PID پرکاربردترین روش کنترل خطی است که توانایی کاهش نوسان و خطای دائمی را دارد.
-
تحلیل پایداری و پاسخ فرکانسی، تضمین عملکرد مطلوب سیستم را فراهم میکند.
-
شبیهسازی با MATLAB یا Python ابزار مهم برای بهینهسازی کنترلکنندهها و بررسی عملکرد واقعی سیستم است.
-
کاربردهای کنترل خطی گستردهاند: موتورهای DC، رباتیک صنعتی، کنترل دما، خودروهای الکتریکی و صنایع شیمیایی.
-
کنترل خطی میتواند با الگوریتمهای هوشمند، کنترل مقاوم و یادگیری ماشین ترکیب شود تا عملکرد سیستم در شرایط واقعی بهینه شود.
پیشنهادات عملی برای ارائه دانشگاهی
-
استفاده از نمودارهای شبیهسازی پاسخ پله و Bode برای نمایش عملکرد PID
-
مقایسه پاسخ سیستمهای P، PI و PID با نمودار خطای ایستا
-
اضافه کردن مثال صنعتی واقعی، مانند کنترل موتور DC یا کوره صنعتی
-
ارائه یک جدول جمعبندی ویژگیها و کاربردهای انواع کنترلها
-
-
Previous Post
پروژه پزشکی
-
Next Post
پروژه اقتصاد